Boosting¶
In this section, we will construct a boosting classifier with the AdaBoost algorithm and a boosting regressor with the AdaBoost.R2 algorithm. These algorithms can use a variety of weak learners but we will use decision tree classifiers and regressors, constructed in Chapter 5.
## Import decision trees
import import_ipynb
import classification_tree as ct;
## Import numpy and visualization packages
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets
1. Classification with AdaBoost¶
The following is a construction of the binary AdaBoost classifier introduced in the concept section. Let’s again use the penguins dataset from seaborn, but rather than predicting the penguin’s species (a multiclass problem), we’ll predict whether the species is Adelie (a binary problem). The data is loaded and split into train vs. test with the hidden code cell below.
## Load data
penguins = sns.load_dataset('penguins')
penguins.dropna(inplace = True)
X = np.array(penguins.drop(columns = ['species', 'island']))
y = 1*np.array(penguins['species'] == 'Adelie')
y[y == 0] = -1
## Train-test split
np.random.seed(123)
test_frac = 0.25
test_size = int(len(y)*test_frac)
test_idxs = np.random.choice(np.arange(len(y)), test_size, replace = False)
X_train = np.delete(X, test_idxs, 0)
y_train = np.delete(y, test_idxs, 0)
X_test = X[test_idxs]
y_test = y[test_idxs]
Recall that AdaBoost fits weighted weak learners. Let’s start by defining the weighted loss functions introduced in the concept section. The helper function get_weighted_pmk() calculates
for each class \(k\). The gini_index() and cross_entropy() functions then call this function and return the appropriate loss.
## Loss Functions
def get_weighted_pmk(y, weights):
ks = np.unique(y)
weighted_pmk = [sum(weights[y == k]) for k in ks]
return(np.array(weighted_pmk)/sum(weights))
def gini_index(y, weights):
weighted_pmk = get_weighted_pmk(y, weights)
return np.sum( weighted_pmk*(1-weighted_pmk) )
def cross_entropy(y, weights):
weighted_pmk = get_weighted_pmk(y, weights)
return -np.sum(weighted_pmk*np.log2(weighted_pmk))
def split_loss(child1, child2, weights1, weights2, loss = cross_entropy):
return (len(child1)*loss(child1, weights1) + len(child2)*loss(child2, weights2))/(len(child1) + len(child2))
In order to incorporate observation weights, we have to make slight adjustments to the DecisionTreeClassifier class. In the class we previously constructed, the data from parent nodes was split and funneled anonymously to one of two child nodes. This alone will not allow us to incorporate weights. Instead, we need to also track the ID of each observation so we can track its weight. This is done with the DecisionTreeClassifier class defined in the hidden cell below, which is mostly a reconstruction of the class defined in Chapter 5.
## Helper Classes
class Node:
def __init__(self, Xsub, ysub, observations, ID, depth = 0, parent_ID = None, leaf = True):
self.Xsub = Xsub
self.ysub = ysub
self.observations = observations
self.ID = ID
self.size = len(ysub)
self.depth = depth
self.parent_ID = parent_ID
self.leaf = leaf
class Splitter:
def __init__(self):
self.loss = np.inf
self.no_split = True
def _replace_split(self, loss, d, dtype = 'quant', t = None, L_values = None):
self.loss = loss
self.d = d
self.dtype = dtype
self.t = t
self.L_values = L_values
self.no_split = False
## Main Class
class DecisionTreeClassifier:
#############################
######## 1. TRAINING ########
#############################
######### FIT ##########
def fit(self, X, y, weights, loss_func = cross_entropy, max_depth = 100, min_size = 2, C = None):
## Add data
self.X = X
self.y = y
self.N, self.D = self.X.shape
dtypes = [np.array(list(self.X[:,d])).dtype for d in range(self.D)]
self.dtypes = ['quant' if (dtype == float or dtype == int) else 'cat' for dtype in dtypes]
self.weights = weights
## Add model parameters
self.loss_func = loss_func
self.max_depth = max_depth
self.min_size = min_size
self.C = C
## Initialize nodes
self.nodes_dict = {}
self.current_ID = 0
initial_node = Node(Xsub = X, ysub = y, observations = np.arange(self.N), ID = self.current_ID, parent_ID = None)
self.nodes_dict[self.current_ID] = initial_node
self.current_ID += 1
# Build
self._build()
###### BUILD TREE ######
def _build(self):
eligible_buds = self.nodes_dict
for layer in range(self.max_depth):
## Find eligible nodes for layer iteration
eligible_buds = {ID:node for (ID, node) in self.nodes_dict.items() if
(node.leaf == True) &
(node.size >= self.min_size) &
(~ct.all_rows_equal(node.Xsub)) &
(len(np.unique(node.ysub)) > 1)}
if len(eligible_buds) == 0:
break
## split each eligible parent
for ID, bud in eligible_buds.items():
## Find split
self._find_split(bud)
## Make split
if not self.splitter.no_split:
self._make_split()
###### FIND SPLIT ######
def _find_split(self, bud):
## Instantiate splitter
splitter = Splitter()
splitter.bud_ID = bud.ID
## For each (eligible) predictor...
if self.C is None:
eligible_predictors = np.arange(self.D)
else:
eligible_predictors = np.random.choice(np.arange(self.D), self.C, replace = False)
for d in sorted(eligible_predictors):
Xsub_d = bud.Xsub[:,d]
dtype = self.dtypes[d]
if len(np.unique(Xsub_d)) == 1:
continue
## For each value...
if dtype == 'quant':
for t in np.unique(Xsub_d)[:-1]:
L_condition = Xsub_d <= t
ysub_L = bud.ysub[L_condition]
ysub_R = bud.ysub[~L_condition]
weights_L = self.weights[bud.observations][L_condition]
weights_R = self.weights[bud.observations][~L_condition]
loss = split_loss(ysub_L, ysub_R,
weights_L, weights_R,
loss = self.loss_func)
if loss < splitter.loss:
splitter._replace_split(loss, d, 'quant', t = t)
else:
for L_values in ct.possible_splits(np.unique(Xsub_d)):
L_condition = np.isin(Xsub_d, L_values)
ysub_L = bud.ysub[L_condition]
ysub_R = bud.ysub[~L_condition]
weights_L = self.weights[bud.observations][L_condition]
weights_R = self.weights[bud.observations][~L_condition]
loss = split_loss(ysub_L, ysub_R,
weights_L, weights_R,
loss = self.loss_func)
if loss < splitter.loss:
splitter._replace_split(loss, d, 'cat', L_values = L_values)
## Save splitter
self.splitter = splitter
###### MAKE SPLIT ######
def _make_split(self):
## Update parent node
parent_node = self.nodes_dict[self.splitter.bud_ID]
parent_node.leaf = False
parent_node.child_L = self.current_ID
parent_node.child_R = self.current_ID + 1
parent_node.d = self.splitter.d
parent_node.dtype = self.splitter.dtype
parent_node.t = self.splitter.t
parent_node.L_values = self.splitter.L_values
## Get X and y data for children
if parent_node.dtype == 'quant':
L_condition = parent_node.Xsub[:,parent_node.d] <= parent_node.t
else:
L_condition = np.isin(parent_node.Xsub[:,parent_node.d], parent_node.L_values)
Xchild_L = parent_node.Xsub[L_condition]
ychild_L = parent_node.ysub[L_condition]
child_observations_L = parent_node.observations[L_condition]
Xchild_R = parent_node.Xsub[~L_condition]
ychild_R = parent_node.ysub[~L_condition]
child_observations_R = parent_node.observations[~L_condition]
## Create child nodes
child_node_L = Node(Xchild_L, ychild_L, child_observations_L,
ID = self.current_ID, depth = parent_node.depth + 1,
parent_ID = parent_node.ID)
child_node_R = Node(Xchild_R, ychild_R, child_observations_R,
ID = self.current_ID + 1, depth = parent_node.depth + 1,
parent_ID = parent_node.ID)
self.nodes_dict[self.current_ID] = child_node_L
self.nodes_dict[self.current_ID + 1] = child_node_R
self.current_ID += 2
#############################
####### 2. PREDICTING #######
#############################
###### LEAF MODES ######
def _get_leaf_modes(self):
self.leaf_modes = {}
for node_ID, node in self.nodes_dict.items():
if node.leaf:
values, counts = np.unique(node.ysub, return_counts=True)
self.leaf_modes[node_ID] = values[np.argmax(counts)]
####### PREDICT ########
def predict(self, X_test):
# Calculate leaf modes
self._get_leaf_modes()
yhat = []
for x in X_test:
node = self.nodes_dict[0]
while not node.leaf:
if node.dtype == 'quant':
if x[node.d] <= node.t:
node = self.nodes_dict[node.child_L]
else:
node = self.nodes_dict[node.child_R]
else:
if x[node.d] in node.L_values:
node = self.nodes_dict[node.child_L]
else:
node = self.nodes_dict[node.child_R]
yhat.append(self.leaf_modes[node.ID])
return np.array(yhat)
With the weighted decision tree constructed, we are ready to build our AdaBoost class. The class closely follows the algorithm introduced in the content section, which is copied below for convenience.
Discrete AdaBoost Algorithm
Define the target variable to be \(y_n \in \{-1, +1 \}\).
Initialize the weights with \(w^1_n = \frac{1}{N}\) for \(n = 1, 2, \dots, N\).
For \(t = 1, \dots, T\),
Build weak learner \(t\) using weights \(\mathbf{w}^t\).
Calculate fitted values \(f^t(\bx_n) \in \{-1, +1\}\) for \(n = 1, 2, \dots, N\). Let \(I^t_n\) equal 1 If \(f^t(\bx_n) \neq y_n\) and 0 otherwise. That is, \(I^t_n\) indicates whether learner \(t\) misclassifies observation \(n\).
Calculate the weighted error for learner \(t\):
\[ \epsilon^t = \frac{\sumN w^t_n I^t_n}{\sumN w^t_n}. \]Calculate the accuracy measure for learner \(t\):
\[ \alpha^t = \log\left(\frac{1-\epsilon^t}{\epsilon^t}\right). \]Update the weighting with
\[ w^{t + 1}_n = w^t_n\exp(\alpha^tI^t_n), \]for \(n = 1, 2, \dots, N\).
Calculate the overall fitted values with \(\hat{y}_n = \text{sign} \left( \sum_{t = 1}^T \alpha^t f^t(\bx_n)\right)\).
class AdaBoost:
def fit(self, X_train, y_train, T, stub_depth = 1):
self.y_train = y_train
self.X_train = X_train
self.N, self.D = X_train.shape
self.T = T
self.stub_depth = stub_depth
## Instantiate stuff
self.weights = np.repeat(1/self.N, self.N)
self.trees = []
self.alphas = []
self.yhats = np.empty((self.N, self.T))
for t in range(self.T):
## Calculate stuff
self.T_t = DecisionTreeClassifier()
self.T_t.fit(self.X_train, self.y_train, self.weights, max_depth = self.stub_depth)
self.yhat_t = self.T_t.predict(self.X_train)
self.epsilon_t = sum(self.weights*(self.yhat_t != self.y_train))/sum(self.weights)
self.alpha_t = np.log( (1-self.epsilon_t)/self.epsilon_t )
self.weights = np.array([w*(1-self.epsilon_t)/self.epsilon_t if self.yhat_t[i] != self.y_train[i]
else w for i, w in enumerate(self.weights)])
## Append stuff
self.trees.append(self.T_t)
self.alphas.append(self.alpha_t)
self.yhats[:,t] = self.yhat_t
self.yhat = np.sign(np.dot(self.yhats, self.alphas))
def predict(self, X_test):
yhats = np.zeros(len(X_test))
for t, tree in enumerate(self.trees):
yhats_tree = tree.predict(X_test)
yhats += yhats_tree*self.alphas[t]
return np.sign(yhats)
The AdaBoost model is finally fit below. To train the model, we supply the training data as well as T—the number of weak learners—and stub_depth—the depth for each tree (our weak learner).
booster = AdaBoost()
booster.fit(X_train, y_train, T = 30, stub_depth = 3)
yhat = booster.predict(X_test)
np.mean(yhat == y_test)
0.9759036144578314
2. Regression with AdaBoost.R2¶
Next, let’s implement AdaBoost.R2, a common boosting algorithm for regression tasks. We’ll again use the tips dataset from seaborn, loaded in the hidden code cell below.
## Import packages
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets
## Load data
tips = sns.load_dataset('tips')
X = np.array(tips.drop(columns = 'tip'))
y = np.array(tips['tip'])
## Train-test split
np.random.seed(1)
test_frac = 0.25
test_size = int(len(y)*test_frac)
test_idxs = np.random.choice(np.arange(len(y)), test_size, replace = False)
X_train = np.delete(X, test_idxs, 0)
y_train = np.delete(y, test_idxs, 0)
X_test = X[test_idxs]
y_test = y[test_idxs]
Since our boosting class will use regression trees for its weak learners, let’s also import the regression tree we constructed in Chapter 5.
## Import decision trees
import import_ipynb
import regression_tree as rt;
Recall that the final fitted values in AdaBoost.R2 are based on a weighted median. Let’s first make a helper function to return the weighted median.
def weighted_median(values, weights):
sorted_indices = values.argsort()
values = values[sorted_indices]
weights = weights[sorted_indices]
weights_cumulative_sum = weights.cumsum()
median_weight = np.argmax(weights_cumulative_sum >= sum(weights)/2)
return values[median_weight]
We can then fit the AdaBoostR2 class. This again follows the algorithm closely, which is again copied below for convenience.
AdaBoost.R2 Algorithm
Initialize the weights with \(w^1_n = \frac{1}{N}\) for \(n = 1, 2, \dots, N\).
For \(t = 1, 2, \dots, T\) or while \(\bar{L}^t\), as defined below, is less than or equal to 0.5,
Draw a sample of size \(N\) from the training data with replacement and with probability \(w^t_n\) for \(n = 1, 2, \dots, N\).
Fit weak learner \(t\) to the resampled data and calculate the fitted values on the original dataset. Denote these fitted values with \(f^t(\bx_{n})\) for \(n = 1, 2, \dots, N\).
Calculate the observation error \(L^t_{n}\) for \(n = 1, 2, \dots, N\):
\[\begin{split} \begin{aligned} D^t &= \underset{n}{\text{max}} \{ |y_{n} - f^t(\bx_{n})| \} \\ L^t_{n} &= \frac{|y_{n} - f^t(\bx_{n})|}{D^t} \end{aligned} \end{split}\]Calculate the model error \(\bar{L}^t\):
\[ \bar{L}^t = \sum_{n = 1}^N L^t_n w^t_n \]If \(\bar{L}^t \geq 0.5\), end iteration and set \(T\) equal to \(t - 1\).
Let \(\beta^t = \frac{\bar{L}^t}{1- \bar{L}^t}\). The lower \(\beta^t\), the greater our confidence in the model.
Let \(Z^t = \sum_{n = 1}^N w^t_n (\beta^t)^{1 - L_n}\) and update the model weights with
\[ w^{t + 1}_n = \frac{w^t_n (\beta^t)^{1 - L_n}}{Z^t}, \]which increases the weight for observations with a greater error \(L^t_n\).
Set the overall fitted value for observation \(n\) equal to the weighted median of \(f^t(\bx_n)\) for \(t = 1, 2, \dots, T\) using weights \(\log(1/\beta^t)\) for model \(t\).
class AdaBoostR2:
def fit(self, X_train, y_train, T = 100, stub_depth = 1, random_state = None):
self.y_train = y_train
self.X_train = X_train
self.T = T
self.stub_depth = stub_depth
self.N, self.D = X_train.shape
self.weights = np.repeat(1/self.N, self.N)
np.random.seed(random_state)
self.trees = []
self.fitted_values = np.empty((self.N, self.T))
self.betas = []
for t in range(self.T):
## Draw sample, fit tree, get predictions
bootstrap_indices = np.random.choice(np.arange(self.N), size = self.N, replace = True, p = self.weights)
bootstrap_X = self.X_train[bootstrap_indices]
bootstrap_y = self.y_train[bootstrap_indices]
tree = rt.DecisionTreeRegressor()
tree.fit(bootstrap_X, bootstrap_y, max_depth = stub_depth)
self.trees.append(tree)
yhat = tree.predict(X_train)
self.fitted_values[:,t] = yhat
## Calculate observation errors
abs_errors_t = np.abs(self.y_train - yhat)
D_t = np.max(abs_errors_t)
L_ts = abs_errors_t/D_t
## Calculate model error (and possibly break)
Lbar_t = np.sum(self.weights*L_ts)
if Lbar_t >= 0.5:
self.T = t - 1
self.fitted_values = self.fitted_values[:,:t-1]
self.trees = self.trees[:t-1]
break
## Calculate and record beta
beta_t = Lbar_t/(1 - Lbar_t)
self.betas.append(beta_t)
## Reweight
Z_t = np.sum(self.weights*beta_t**(1-L_ts))
self.weights *= beta_t**(1-L_ts)/Z_t
## Get median
self.model_weights = np.log(1/np.array(self.betas))
self.y_train_hat = np.array([weighted_median(self.fitted_values[n], self.model_weights) for n in range(self.N)])
def predict(self, X_test):
N_test = len(X_test)
fitted_values = np.empty((N_test, self.T))
for t, tree in enumerate(self.trees):
fitted_values[:,t] = tree.predict(X_test)
return np.array([weighted_median(fitted_values[n], self.model_weights) for n in range(N_test)])
Again, we fit our booster by providing training data in addition to T—the number of weak learners—and stub_depth—the depth for our regression tree weak learners.
booster = AdaBoostR2()
booster.fit(X_train, y_train, T = 50, stub_depth = 4, random_state = 123)
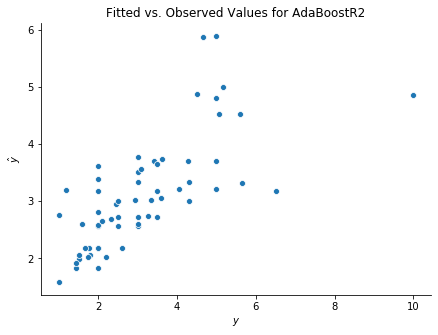
fig, ax = plt.subplots(figsize = (7,5))
sns.scatterplot(y_test, booster.predict(X_test));
ax.set(xlabel = r'$y$', ylabel = r'$\hat{y}$', title = 'Fitted vs. Observed Values for AdaBoostR2')
sns.despine()